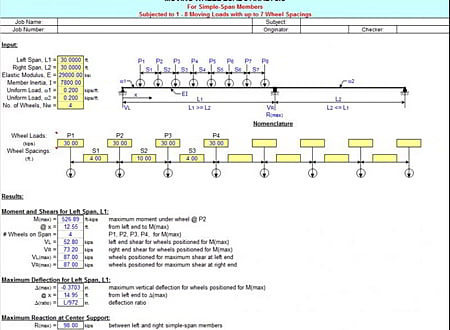
MOVLOADS is a spreadsheet program written in MS-Excel for the purpose of analysis of simple-span members subjected to from one up to eight moving wheel loads with up to seven wheel spacings. Specifically, the maximum moment and location from the left end of the member and wheel postioning, the maximum end shears, the maximum deflection, and the maximum center support reaction for two (2) adjacent simple-span members are calculated.

Program Assumptions and Limitations:

1. The following references were used in the development of this program (see below):

• a. "Modern Formulas for Statics and Dynamics, A Stress-and-Strain Approach" by Walter D. Pilkey and Pin Yu Chang, McGraw-Hill Book Company (1978), pages 11 to 21.
• b. AISC 9th Edition Allowable Stress (ASD) Manual (1989), pages 2-298 and 2-310.

2. This program uses the three (3) following assumptions as a basis for analysis:

• a. Beams must be of constant cross section (E and I are constant for entire span length).
• b. Deflections must not significantly alter the geometry of the problem.
• c. Stress must remain within the "elastic" region.

3. To determine the value of the maximum moment and location from the left end of the left span for either only one (1) or two (2) wheel loads, those values are calculated directly by formulas.

4. To determine the value of the maximum moment and location from the left end of the left span for three (3) up to eight (8) wheel loads, the group of wheel loads is positioned with wheel load P1 situated directly over the left support. Then the group is moved to the right in 1/200*span increments, and the left and right reactions as well as the moments under each of the wheel loads are calculated. In moving the group of wheel loads incrementally from left to right, any wheels that would drop off of the span are done so. Then this entire procedure is mirrored for the opposite direction, from right to left.

CAUTION: When the sum of all of the wheel spacings > L1, then user must input all other possible groupings of wheel loads/spacings <= L1 to assure that the maximum moment has been determined. The only exception to this is the case for all equal wheel loads with all equal wheel spacings. The Left Span (L1) must always be >= the Right Span (L2).

5. To determine the value of the maximum reaction at the center support of 2 adjacent simple spans, the group of wheels is positioned with the right most wheel load situated directly over the center support. Then the group is moved to the right, one wheel position at a time, until the left most wheel load, P1, is positioned directly over the center support. In moving the group of wheel loads one wheel position at a time from left to right, any wheels at either end that would drop off of the span(s) are done so.

6. The calculated value for the maximum deflection is determined from dividing the beam into fifty (50) equal segments with fifty-one (51) points, and including all of the point load locations as well. (Note: the actual point of maximum deflection is where the slope = 0.)

7. The user is given the ability to input two (2) specific locations from the left end of the beam to calculate the shear, moment, slope, and deflection.

* MOVLOADS download link provides freeware version of the software.

Single-Span & Continuous-Span Beam Analysis

BEAMANAL is a MS-Excel spreadsheet workbook for the analysis of single-span beams (simple, propped, fixed, or cantilever) and continuous beams of up to 5 spans.

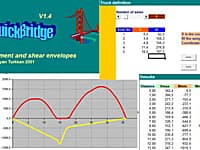
Moving truck analysis for bridges with simple or continuous spans

Moving truck (up to 20 axles) analysis for bridges with simple or continuous spans (up to 5). Envelopes (M & V) and support reactions.

Inelastic Analysis of Structural Members Subjected to Blast-Induced Shock Waves

RCBlast was developed to conduct dynamic inelastic response history analysis of reinforced concrete elements subjected to blast-induced shock waves.

BS 5400, BD 21 and BD 86

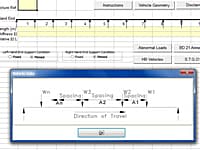
Abnormal Load Vehicles, HB Vehicles, BD21 Annex D Vehicles and BD86 STGO Vehicles are analysed as moving loads across a single or multi-span continuous line beam to determine critical bending moments and shear forces.

Asphalt Thickness Design for Highways, Airports, Heavy Wheel Loads

An integrated pavement design suite for highways, streets, parking lots, airports, and industrial facilities supporting heavy wheel loads.

Submit a review about MOVLOADS software with your social media profile